2020年(令和2年)3月4日に実施された北海道公立高校入試、裁量問題の数学、解答と解説です。
結論。
今年も裁量問題とは何なのか、よくわからない出題だった。
(去年の激甘設定よりはマシ)
表紙

大問1
なんてことありません。
山場もなくオーソドックスな出題なので、しっかり得点を稼ぎましょう。
| 問1 | 難易度│★☆☆☆☆ | 因数分解→式の値を求める | ||
| 問2 | 難易度│★★☆☆☆ | 確率 | ||
| 問3 | 難易度│★☆☆☆☆ | 作図 | ||
| 問4(1) | 難易度│★☆☆☆☆ | 式であらわす | ||
| 問4(2) | 難易度│★★☆☆☆ | 2次方程式の文章題 |


大問2
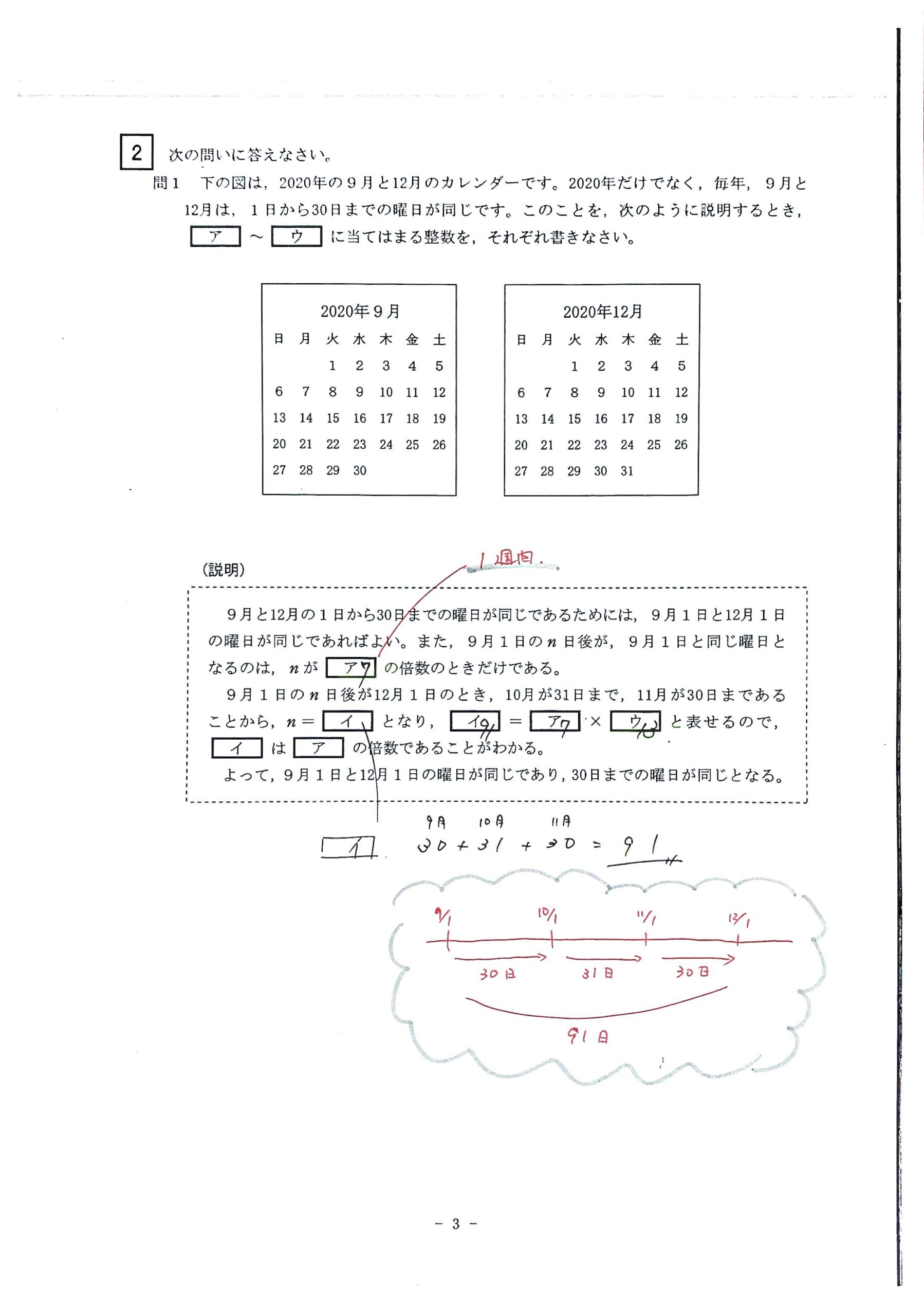
カレンダーと倍数の関係が、やや取っかかりにくかったか。
特に問2は、今年の数学で一番難しかった。曜日の規則性がつかみにくい。
| 問1 | 難易度│★★★☆☆☆ | 式の説明 | ||
| 問2 | 難易度│★★★★★ | 規則性 |

大問3
問1〜3まですべて「座標を文字であらわす」ことさえ出来れば解ける。
基本の出題なので、上位校だと差はつかない。
| 問1 | 難易度│★☆☆☆☆ | 二次関数:座標を文字であらわす | ||
| 問2 | 難易度│★★☆☆☆ | 二次関数:直線の式を求める | ||
| 問3 | 難易度│★★★☆☆ | 二次関数:傾きから座標を求める |


大問4
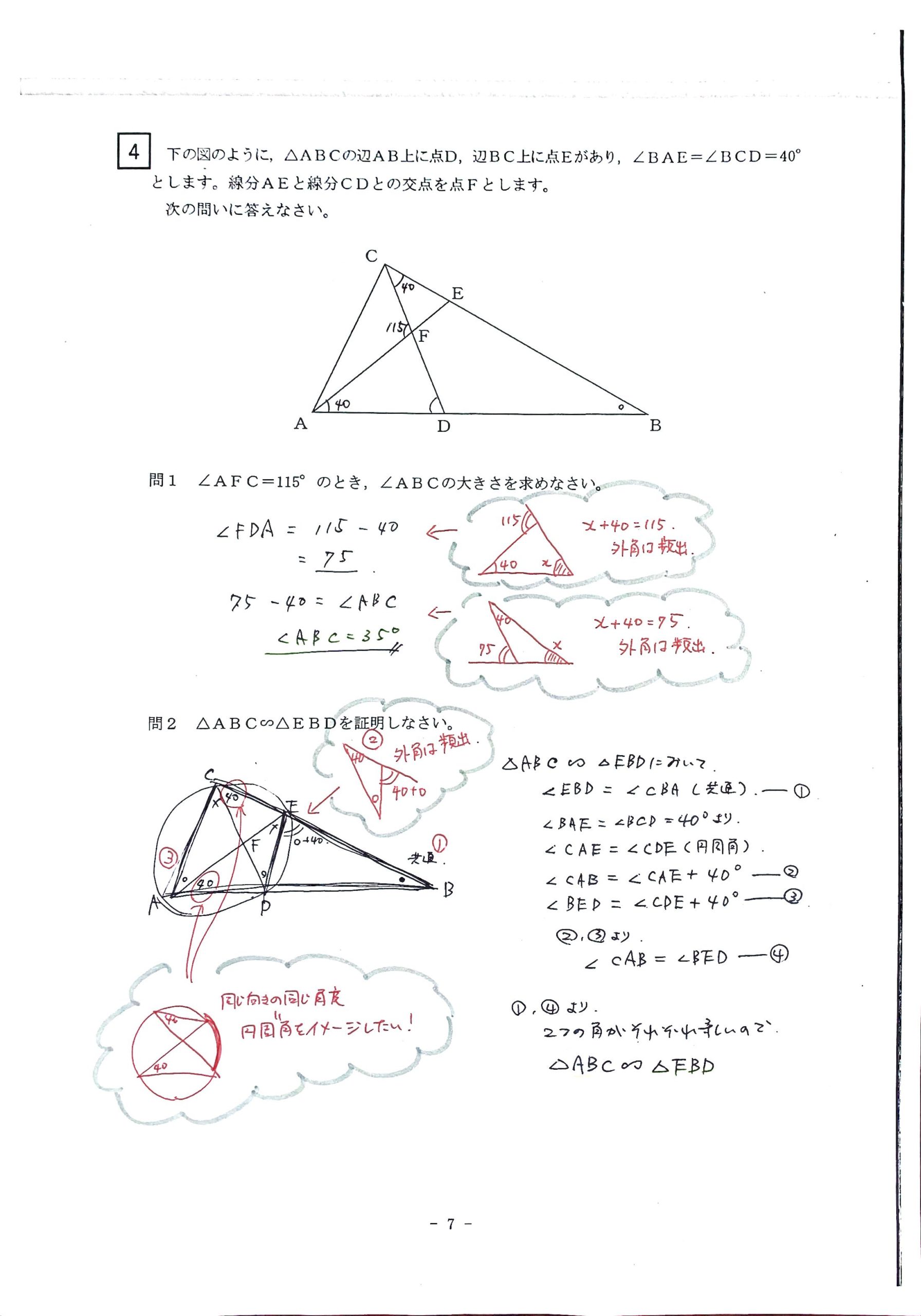
「三角形の外角を見抜くこと」が重要だった。
問2に関しては、円周角に気づくことが出来るかどうかで運命がわかれる。
| 問1 | 難易度│★★☆☆☆ | 角度を求める | ||
| 問2 | 難易度│★★★★☆ | 相似の証明 |
大問5(裁量問題)
裁量問題らしい難しさはなかった。
今年もまた、裁量問題とは何なのか、よくわからない出題であった。
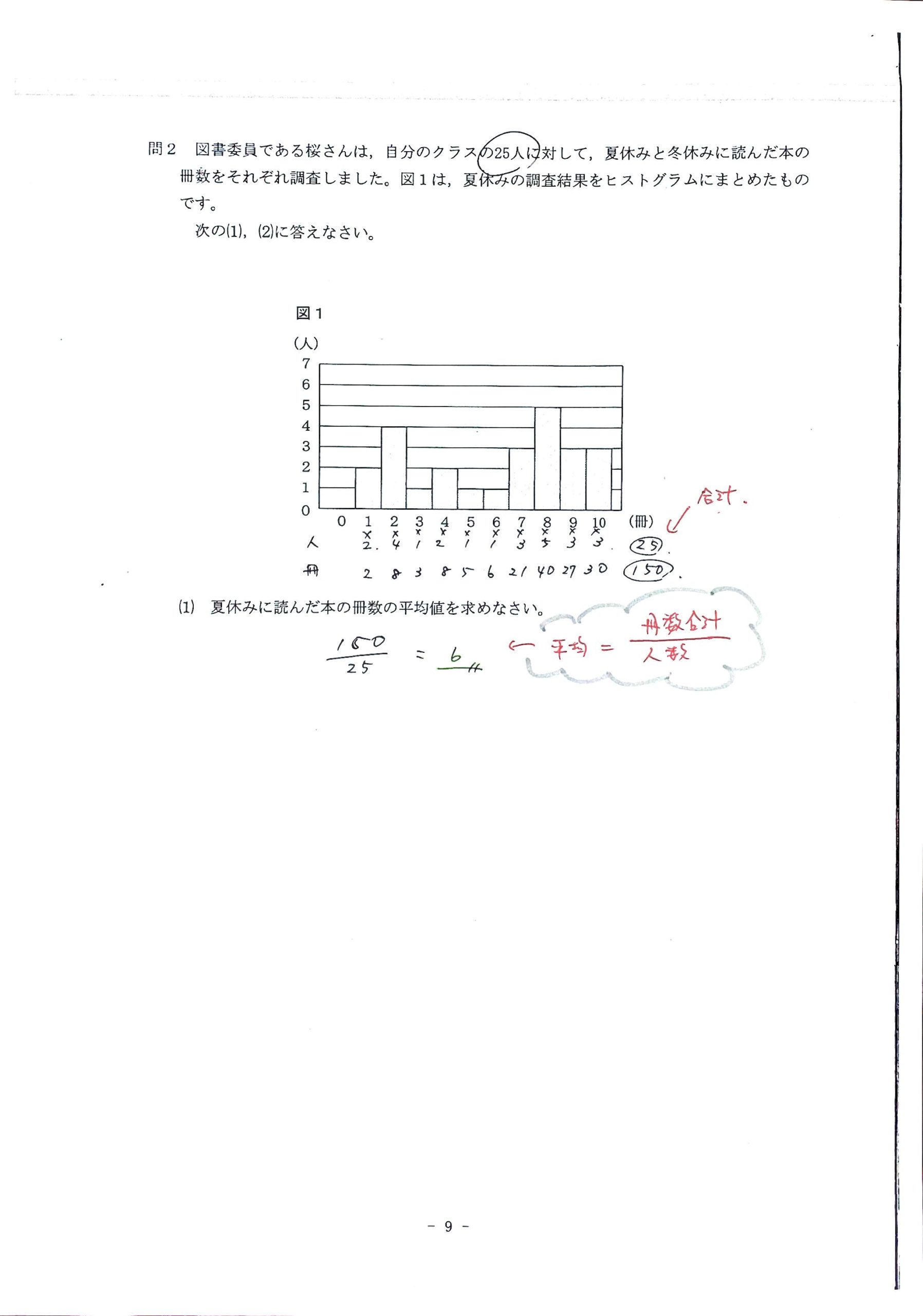
問2(2)は、「冬の中央値が8冊」というヒントを読み取れるかどうかが勝負。
問3(2)は、図形らしいヒネリが足りなく、つまらない問題だった。
| 問1(1) | 難易度│★☆☆☆☆ | 1次関数の利用:道のりを求める | ||
| 問1(2) | 難易度│★★★☆☆ | 1次関数の利用:方程式の立式 | ||
| 問2(1) | 難易度│★☆☆☆☆ | 平均値 | ||
| 問2(2) | 難易度│★★★★☆ | ヒストグラムと中央値/平均値 | ||
| 問3(1) | 難易度│★☆☆☆☆ | 三平方の定理:線分の長さ | ||
| 問3(2) | 難易度│★★★★☆ | 三平方の定理:回転体と体積 |



来年以降の受験生へ
昨年、今年の傾向を見ていると、問題の難易度を探りながら慎重に問題を作っているように感じます。
その結果、『難しい問題が解けるか』ではなく、『どれだけ正確に問題を解き、失点しないか』で差がつく入試になっています。
積極的に難しい問題や未知の問題にチャレンジする一方で、泥臭く練習を重ね、基礎基本をしっかり固めることが求められます。
現中1から始まる【入試100点満点への変更】が控えている今、大きく出題を変えることは想像できないので、同じような傾向が続くような気がしています。
北海道札幌市で塾の先生をしつつ、家庭教師の派遣・Webサイト作成・チラシ作成など、幅広くお仕事させていただいています。
『情報発信の可能性を探りたい』などとゆる〜く考えながら、自由気ままにブログを綴っています。
まつブロ│個人の情報発信 https://mats39.com
個別指導北大コーチ│運営している塾 http://hokudaicoach.com
Twitter│ボソッとつぶやき https://twitter.com/matsdesu




コメント